Parse |
The Parse processor is an extremely powerful tool for the understanding and structural improvement of data. It allows you to analyze and understand the semantic meaning of data in one or many attributes, by applying both manually configured business rules, and artificial intelligence. It then allows you to use that semantic meaning in rules to validate and optionally restructure the data. For example, Parse allows you to recognize names data that is wrongly captured in address attributes, and optionally map it to new attributes in a different structure.
The Parse processor can be configured to understand and transform any type of data. For an introduction to parsing in OEDQ, see the Parsing Concept Guide.
For a description of the use and functionality of the Parse processor, read on in this topic.
The Parse processor has a variety of uses. For example, you can use Parse to:
The Parser runs in several steps. Each step is fully explained in the Configuration section below. However, the processing of the parser can be summarized as follows:
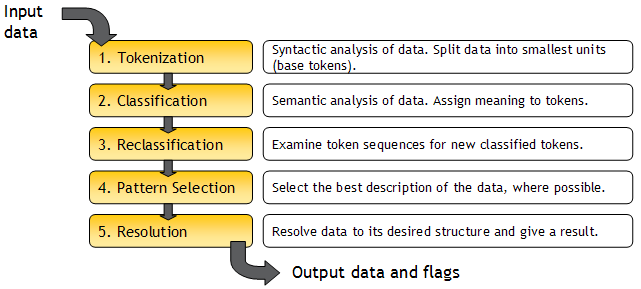
To understand how the Parse processor works as a whole, it is useful to follow an example record through it. In this example, we are parsing an individual name from three attributes - Title, Forenames, and Surname.
Example Input Record
The following record is input:
![]()
Tokenization
Tokenization tokenizes the record as follows, recognizing the tokens 'Mr', 'Bill', 'Archibald' and 'SCOTT' and assigning them a token tag of <A>. It also recognizes the space between 'Bill' and 'Archibald' as a token and assigns it a token tag of <_>. Note that Tokenization always outputs a single pattern of base tokens. In this case, the pattern is as shown below (from the Tokenization view):
![]()
Classification
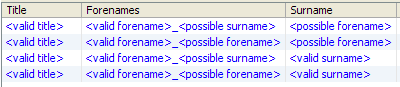
Classification then classifies the tokens in the record using classification rules with lists of names and titles. As some of the names appear on multiple lists, some of the tokens are classified in multiple ways - for example, the token 'Archibald' is classified both as a <possible forename> and as a <possible surname>, and the token 'SCOTT' is classified both as a <possible forename> and as a <valid surname>. As a result, Classification outputs multiple classification patterns, as shown below in the Classification view:
Reclassification
As above, we now have multiple descriptions of the data. However, we might decide to apply the following Reclassification rule to the Forenames attribute to denote that because the token 'Archibald' follows a valid forename, we can be confident that it represents a middle name:
![]()
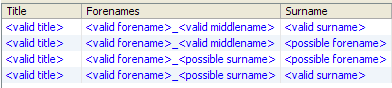
This rule acts on the pattern '<valid forename>(<possible forename>)' in the Forenames attribute, which affects the second and fourth classification patterns above. In the Reclassification view, we now have the following four patterns; that is, four possible descriptions of the data:
|
Note:The Reclassification view will only show the patterns that have been pre-selected for entry into the Selection process. Pre-selection is a non-configurable first step in the selection process which eliminates patterns containing too many unclassified tokens. The pre-selection process first surveys all the patterns generated so far, and determines the minimum number of unclassified tokens present in any one pattern. Next, any patterns with more than that number of unclassified tokens are eliminated. In the example above, none of the patterns contain any unclassified tokens, so the minimum number of unclassified tokens is zero. Since none of the patterns contain more than zero unclassified tokens, none of the patterns are eliminated in the pre-selection process. |
Selection
Selection now attempts to pick the best overall pattern from the four possibilities. In this case, we can see that the first pattern above is the strongest as all of its token classifications have a result of 'valid'. By scoring each of the patterns using the default selection rules, therefore, the first pattern is selected and displayed in the Selection view:
![]()
Resolution
If we accept that the selected pattern is a good description of the record, we can then resolve the pattern to output attributes, and assign a result. In this case, we can do this by right-clicking on the selected pattern above and selecting Resolve... to add an Exact resolution rule.
We use the default output assignments (according to the classifications made), and assign the pattern a Pass result, with a Comment of 'Known name format':
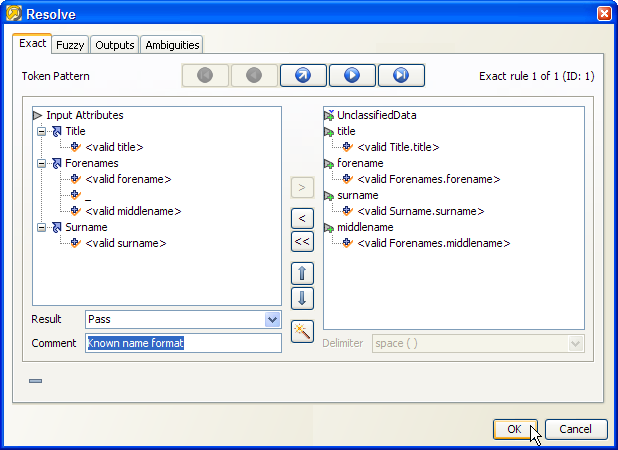
After re-running Parse with this rule, we can see that the rule has resolved the input record:
![]()
Finally, we can drill down to the record and see that data has correctly been assigned to output attributes according to the resolution rule:
![]()
Parse is an advanced processor with several sub-processors, where each sub-processor performs a different step of parsing, and requires separate configuration. The following sub-processors make up Parse, each performing a distinct function as described below.
Click on the sub-processor for detailed information about each step, and for configuration instructions:
Advanced Options
The Parser offers two modes of execution in order to provide optimized performance where some of the results views are not required.
The two modes are:
Parse and Profile (the default mode) should be used when first parsing data, as the parser will output the Token Checks and Unclassified Tokens results views, which are useful when still in the process of defining the parsing rules, by creating and adding to lists used for classification.
Parse mode should be used when the classification configuration of the parser is complete, and optimal performance is needed. Note that the Token Checks and Unclassified Tokens views are not produced when running in this mode.
All options are configurable within each sub-processor.
The output data attributes are configurable in the Resolve sub-processor.
|
Flag attribute |
Purpose |
Possible Values |
|
[Attribute name].SelectedPattern |
Indicates the selected token pattern for the record |
The selected token pattern |
|
[Attribute name].BasePattern |
Indicates the base token pattern for the record, output from tokenization (if using the parser purely to generate this pattern) |
The base token pattern |
|
ParseResult |
Indicates the result of the parser on the record. |
Unknown/Pass/Review/Fail |
|
ParseComment |
Adds the user-specified comment of the record's resolution rule. |
The comment on the resolution rule that resolved the record |
The Parse processor's results may be published to the Dashboard.
The following interpretation of results is used by default:
|
Result |
|
|
Pass |
Pass |
|
Review |
Warning |
|
Fail |
Alert |
|
Execution Mode |
Supported |
|
Batch |
Yes |
|
Real time Monitoring |
Yes |
|
Real time Response |
Yes |
The Parse processor produces a number of views of results as follows. Any of the views may be seen by clicking on the Parse processor in the process. The views may also be seen by expanding the Parse processor to view its sub-processors, and selecting the sub-processor that produces the view.
Base Tokenization View (produced by Tokenize)
This view shows the results of the Tokenize sub-processor, showing all the distinct patterns of Base Tokens across all the input attributes. The patterns are organized by frequency.
|
Note:Each record has one, and only one, base token pattern. Many records have the same base token pattern. |
|
Statistic |
Meaning |
|
For each input attribute |
The pattern of base tokens within the input attribute Note that rows in the view exist for each distinct base token pattern across all attributes |
|
The number of records with the distinct base token pattern across all the input attributes |
|
|
% |
The percentage of records with the distinct base token pattern across all the input attributes |
Token Checks View (produced by Classify)
This views shows the results of the Classify sub-processor, showing the results of each token check within each input attribute.
|
Statistic |
Meaning |
|
Attribute |
The attribute to which the token check was applied |
|
Classifier |
The name of the token check used to classify tokens |
|
Valid |
The number of distinct tokens that were classified as Valid by the token check |
|
Possible |
The number of distinct tokens that were classified as Possible by the token check |
Drill down on the Valid or Possible statistics to see a summary of the distinct classified tokens and the number of records containing them. Drill down again to see the records containing those tokens.
Unclassified Tokens View (produced by Classify)
|
Statistic |
Meaning |
|
Attribute |
The input attribute |
|
Unclassified Tokens |
The total number of unclassified tokens in that attribute |
Drill down on the Unclassified Tokens to see a list of all the unclassified tokens and their frequency. Drill down again to see the records containing those tokens.
Classification View (produced by Classify)
This view shows a list of all the generated token patterns after classification (but before reclassification). There may be many possible patterns for each input record.
|
Statistic |
Meaning |
|
For each input attribute |
The pattern of tokens across the attribute. Note that rows in the view exist for each distinct token pattern across all attributes. |
|
Count |
The number of records where the token pattern is a possible description of the data. Note that the same record may have many possible token patterns in this view, and each token pattern may describe many records. |
|
% |
The Count expressed as a percentage of all the possible token patterns across the data set. |
Reclassification Rules View (produced by Reclassify)
This view shows a list of all reclassification rules, and how they have affected your data.
|
Statistic |
Meaning |
|
The id of the reclassification rule. The ids are auto-assigned. The id is useful where you have dependencies between rules - see the Precedents statistic below. |
|
|
Rule Name |
The name of the reclassification rule. |
|
Attribute |
The attribute to which the reclassification rule was applied. |
|
Look for |
The token pattern used to match the rule |
|
Reclassify as |
The target token of the reclassification rule |
|
Result |
The classification level (valid or possible) of the reclassification rule |
|
Records affected |
The number of records affected by the rule |
|
Patterns affected |
The number of classification patterns affected by the rule |
|
Precedents |
The number of other reclassification rules that preceded this rule before it could operate. For example, if you reclassify the <A> as <B> in one rule, and <B> to <C> in another rule, the first rule is a precedent of the second. Note that even reclassification rules that did not affect any records may have precedents, as these are calculated logically. |
Reclassification View (produced by Reclassify)
This view shows a list of all the generated token patterns after reclassification (but before selection). There may be many possible patterns for each input record. The view presents all of the possible patterns and their frequency across the whole data set, before the Select step attempts to select the best pattern of each input record.
|
Note:The data in this view may itself be used to drive which pattern to select; that is, it is possible to configure the Select step to select the pattern for a record by assessing how common it is across the data set. See the configuration of the Select sub-processor. |
|
Statistic |
Meaning |
|
For each input attribute |
The pattern of tokens across the attribute. Note that rows in the view exist for each distinct token pattern across all attributes. |
|
Count |
The number of records where the token pattern is a possible description of the data. Note that the same record may have many possible token patterns in this view, and each token pattern may describe many records. |
|
% |
The Count expressed as a percentage of all the possible token patterns across the data set. |
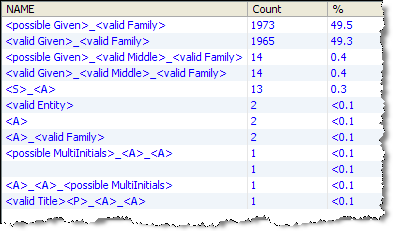
Selection View (produced by Select)
After the Select step, each input record will have a selected token pattern.
This view shows a view of the selected patterns across the data set, and their frequency of occurrence.
|
Note: Where the selection of a single token pattern to describe a record is not possible, because of ambiguities in selection, the pattern with the ambiguity (or ambiguities) is shown along with the number of records that had the same ambiguity; that is, the same set of potential patterns that selection could not choose between. |
|
Statistic |
Meaning |
|
For each input attribute |
The pattern of tokens across the attribute Note that rows in the view exist for each distinct token pattern across all attributes. |
|
The numeric identifier of the exact resolution rule (if any) that resolved the token pattern |
|
|
The numeric identifier of the fuzzy resolution rule (if any) that resolved the token pattern |
|
|
Count |
The number of records where the token pattern was selected as the best description of the data |
|
% |
The percentage of records where the token pattern was selected |
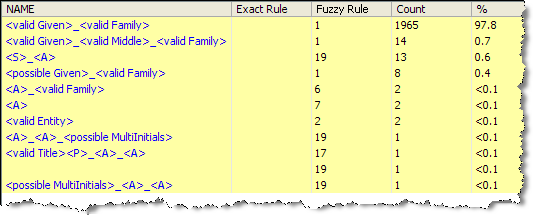
Resolution Rule View (produced by Resolve)
This view shows a summary of the resolutions made by each Resolution Rule. This is useful to check that your rules are working as desired.
|
Statistic |
Meaning |
|
ID |
The numeric identifier of the rule as set during configuration. |
|
Rule |
The type of rule (Exact rule or Fuzzy rule) |
|
Result |
The Result of the rule (Pass, Review or Fail) |
|
Comment |
The Comment of the rule |
|
Count |
The number of records that were resolved using this rule. Click on the Additional Information button in the Results Browser to show this as a percentage. |
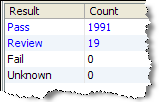
Result View (produced by Resolve)
|
Statistic |
Meaning |
|
Pass |
The total number of records with a Pass result |
|
Review |
The total number of records with a Review result |
|
Fail |
The total number of records with a Fail result |
|
Unknown |
The number of records where Parse could not assign a result |
The following output filters are available from the Parse processor:
In this example, a complete Parse configuration is used in order to understand the data in a single NAME attribute, and output a structured name:
Base Tokenization view
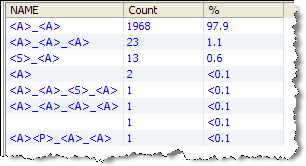
Token Checks view
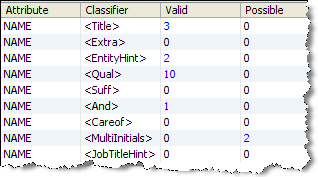
Classification view

Unclassified Tokens view
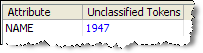
Reclassification Rules view
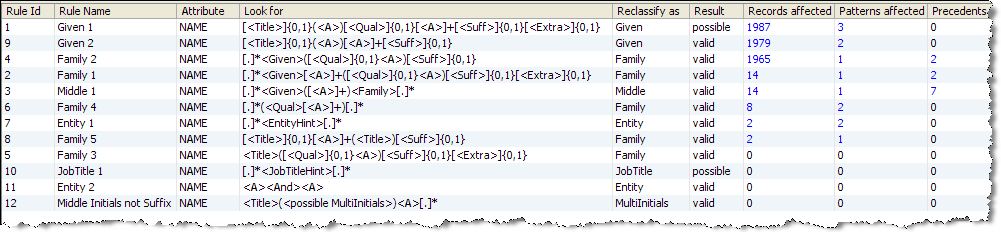
Reclassification view
Selection view
Resolution Rule view

Results view
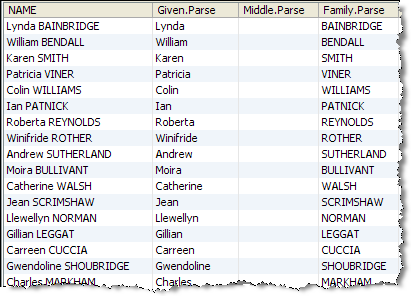
Drill down on Pass results
Oracle ® Enterprise Data Quality Help version 9.0
Copyright ©
2006,2011 Oracle and/or its affiliates. All rights reserved.