Understanding Digital Certificates and Code Signing
Aurelio Garcia-Ribeyro
Director Product Management Java SE
2018-01-26
This document provides a somewhat simplified explanation [1] of the technology behind code signing and digital certificates.
Code signing relies on digital certificates to do its job. To understand certificates and how they are used we need a basic understanding of some concepts: Symmetric and Asymmetric Encryption, and Hashing.
Symmetric and Asymmetric Encryption, and Hashing.
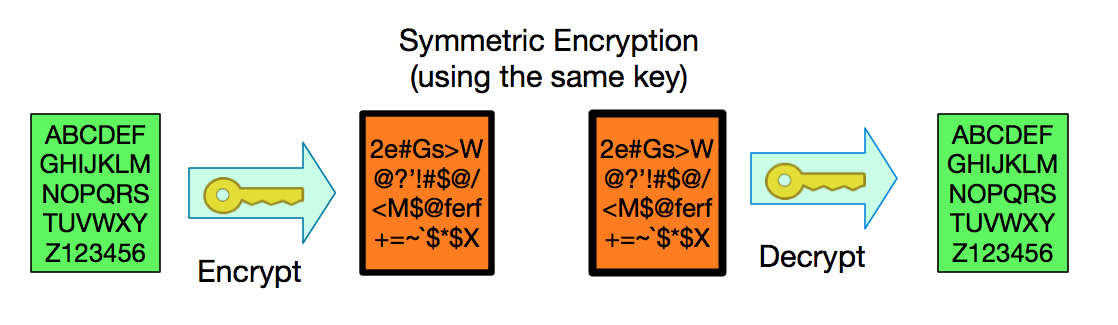
Symmetric Encryption
Whenever we need to protect information it is common practice to encrypt it. This means encoding the information in a way that is not easy to understand unless you know how to translate it.For example, instead of writing “GOOD MORNING” I could replace every letter with a letter that is 3 letters earlier in the alphabet, so “G” becomes “D”, “O becomes L”, etc. and write instead “DLLA JLOKFKD”. [2]
The encrypted message has all of the information of the original message but you need to know the encrypting algorithm (shift letters by a given number) and the encryption key (how many positions to shift) to be able to get the original message back.
We could have used a more complicated “key” like: “The first letter shifts 8 positions, second letter 12 positions, third letter 5 positions. Repeat the “8-12-5” sequence for every group of 3 letters until you encode the whole message”. Even with such a simple algorithm a long enough and random enough key could create something difficult to decipher without the key.
In modern cryptography, it is common that the algorithm used for encryption is known and written along the encrypted message –so authorized users know how to decrypt. The message remains safe only as long as we safeguard the key.
Even without knowing the key it is sometimes possible to decrypt a message.
It might be possible to “brute force” the solution. If the key is small enough a computer could try all possible combinations rather quickly. If there are only a few million combinations for the key, a modern computer could try them all and guess the result in less than a minute.
Mathematicians and researchers are constantly looking for weakness in encryption algorithms, if they find one it might be possible to decrypt the original message without guessing the key or diminish the number of possible keys making a brute-force attack possible.
Since computer power grows over time, and weakness are discovered in previously “safe” algorithms, we must assume that anything considered secure now will not always be secure. Therefore, cryptography comes with expiration dates.
Asymmetric Encryption
In our encryption example above we shifted letters “3 spaces”. The same value/key that we used for encrypting is used for decrypting. If you shifted 3 spaces to the right for encrypting, just shift 3 to the left for decrypting. This type of encryption, where the same key is used for encrypting and decrypting, is called symmetric encryption and has the benefit of being fast and taking relatively few resources to compute. Symmetric encryption has the drawback that you have to share the key used for encrypting with everyone authorized to decrypt.Around 1970, mathematicians and researchers came up with a method of encryption in which two seemingly unrelated values [3] could be used for encrypting/decrypting in such a way that if you encrypt with one value you can only decrypt with the other value and vice-versa. This is known as Asymmetric Encryption.
Asymmetric Encryption is the basis of what is called Public-Key Cryptography.
When compared with symmetric encryption asymmetric encryption takes a lot more processing power, making it slower and more expensive, but has the benefit that if I keep one of the values to myself (let’s call it private key because... well that’s what it’s called!) I can share the other value (you guessed it: the public key [4]) with everyone in the world and have the basis for code signing and TLS authentication.
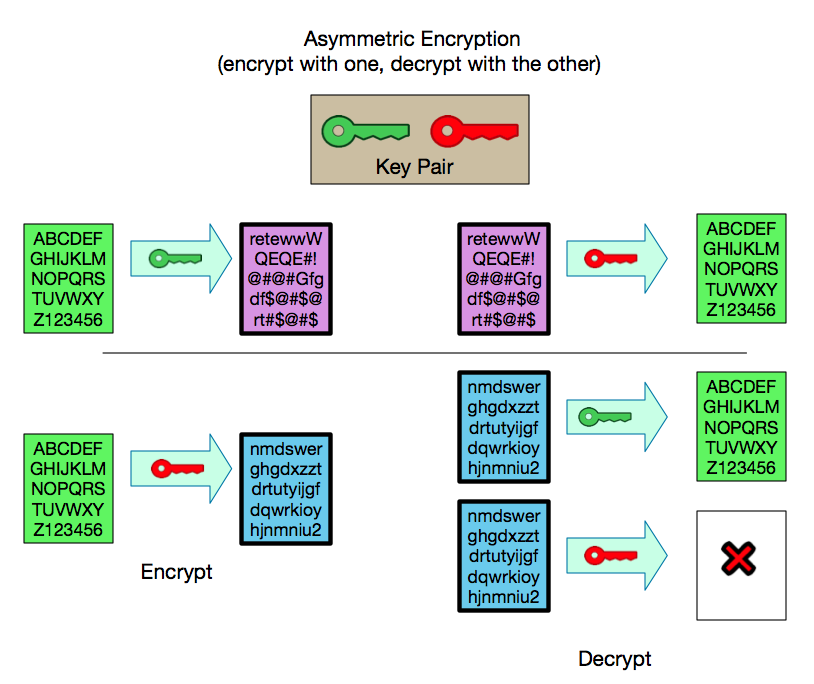
The possibility of keeping one of the keys secret and making the other public means that I can do two important things by sharing the public key with everyone:
1) Everyone can then use the public key to encrypt anything [5] so that only the owner of the matching private key can decrypt it. This ensures a secure “one-way” communications.
2) The owner of the private key can use it to confirm that they encrypted something. Anything that can be decrypted with a public key could only have been encrypted with the corresponding private key.
This is the cornerstone of digital signatures.
Hashing
Another useful technique used in cryptography is to calculate a unique [6] value for each message. This value is called a hash or a checksum.Hashing is a one-way function. Unlike encrypted data, hashes of data do not contain all the information needed to re-create the original input. You can calculate the hash for any message but there is no way to get back the original message if all you have is the hash.
Good hashing functions will produce large variations in the result given even very small changes in the data. In some hashing the resulting value will be of the same size regardless of how large or short the input is.
For example, a commonly used hash function is SHA-256 which produces a 256-bit hash (writing this in hexadecimal requires 64 characters).
Here is the SHA256 checksum for two similar short texts:
| Input Text | SHA256 Checksum |
|---|---|
| Hello | 185f8db32271fe25f561a6fc938b2e264306ec304eda518007d1764826381969 |
| HellO | 4ff7975b53db6c029d88f6ac67bd78d12fed72cdb2e252a26556d594b87bc9d8 |
Simply by changing the last “o” in Hello to upper case the checksum or hash is very different.
The SHA256 checksum of large binaries looks similar to that of the small examples:
| Input File | SHA256 Checksum |
|---|---|
| OpenJDK 9.0.1: package hosted on Java.net approx. 200 MB | a312ea3c51940361af738fda809e08e16972ae9dd314cb087e0d31e251b416a3 |
| Ubuntu download ubuntu-16.04.3-desktop-amd64.iso approx. 1.5 GB | 1384ac8f2c2a6479ba2a9cbe90a585618834560c477a699a4a7ebe7b5345ddc1 |
In the previous examples. Knowing the checksum for an Ubuntu download doesn’t let you “re-create” the complete download. You can’t even tell if you are looking at the checksum for a large file or that of a small value.
Although it is fairly straight forward and relatively fast to compute the checksum for a given value, the opposite: guessing an input that would produce a given checksum, is not possible [7].

Hashing is also used for other non-cryptographic applications like checking that something was transmitted correctly, creating efficient ways of indexing data, and storing passwords [8] securely.
Digital Signing
The idea of digital-signing is straight forward:- Take anything that you want to sign and compute its checksum or hash.
- Generate a private/public key and use the private key to encrypt the checksum/hash that you have calculated for the input [9]. Remember: anything encrypted with the private key can only be decrypted with the corresponding public key.
- Ship the information and include alongside the encrypted checksum (“The Signature”) and the public key to validate it.

If later, someone wants to know if the information they received remains unchanged, they can compute the checksum for the information. Let’s call this the “Calculated checksum”.
Then, using the public key they can decrypt the encrypted checksum that came with the information. Let’s called this the “Signed checksum”.
If the “Calculated checksum” and the “Signed checksum” match this tells us that 1) The information hasn’t changed (since the checksums are the same) and 2) that only someone with access to the private key that matches the public key could have created that signature.

Note that signing the data does not encrypt it. The idea of signing is not to keep the information secret but simply to ensure that the information has not been altered and that it was signed by someone who held a particular private key.
The problem is: how do we know if a public key really matches the private key from a particular person or company?
We need someone or something who can vouch for the authenticity of the public key…
Certificate Authorities
Certificate Authorities (CAs) are entities that act as trusted third parties. Once you have a trusted authority we can have use them to establish a “chain” of trust as follows:- The person that wants to sign something needs to convince the certificate authority that they are who they claim to be.
- End users like you and I trust those certificate authorities and accept that “if this CA says they verified a user then we can trust that they did.”
Different Certificate Authorities have different processes for issuing a certificate but they all go something like this:
A person or company creates, in their own computer, a private/public key combination using some program available in most operating systems or by downloading a program specifically for this purpose.
That person or company saves the private key. They won’t share this with anybody, not even the Certificate Authority.
The person (let’s call them person from now on. It gets long to keep writing “person or company”) contacts the CA who will issue the certificate.
The CA will ask the person for the public key that her or she generated in the previous step, details on what they want the certificate for (e.g. code signing, TLS authentication, encrypting email, etc.), a name to put in the certificate, an address or location, the domain to authenticate, etc.
The CA will also ask you for details to validate that you are indeed who you claim to be. They might require a copy of your driver license, or a company’s articles of incorporation or, if you are asking for a TLS certificate, they might ask you to prove that you control the domain name for which you want the certificate by putting some text of their choosing in your website.
The exact details of what you will need to provide will change depending on what you will need the certificate for and which CA you use. A certificate for encrypting email for a single address will usually need less scrutiny than a TLS certificate for a web domain with the name of a well-known bank. This is why a digital certificate has a list of things for which it’s good for and will not be trusted for other purposes.
The CA will also want to know how long to issue the certificate for. Most Certificate Authorities will issue certificates for 1 to 3 years. They will usually charge for their services and charge higher for certificates that expire later.
Once they are satisfied that you are who you claim to be and have met all their requirements they will produce a document that will contain:
- Some of the given information (name, address, URL or email, etc.)
- What the certificate is valid for (e.g. code signing and mail encryption)
- When the certificate is being issued, and until when will it be considered valid.
- The public key that you provided them
- Information about the issuing Certificate Authority.
The question then becomes, how do you get the CA’s public key so you can verify that they created the digital certificate?
Certificate Authorities work with the developers of operating systems, browsers, and runtimes like the Java Runtime (JRE). The developers of those programs evaluate each candidate Certificate Authority by looking into auditors’ reports, industry certifications, how well established they are, and many other criteria that varies for each program. If they think a CA is trustworthy and meets their particular needs the developers of the operating systems, browsers, and runtimes include the CA’s public key –which they receive directly from the CA’s- in their programs.
You can see what Certificate Authorities are included in your browsers. For example, in Firefox on macOS you can type “about:preferences#privacy” into the address bar (on Windows use "about:preferences#advanced") and scroll to the bottom where you will find the “Certificates” section. You can choose to view the complete list of trusted CAs’ certificates and see the details of what is in each certificate.

All browsers, some operating systems, and a few runtimes have a similar –though not necessarily exactly the same- lists of “Trusted Certificate Authorities”.
A browser or operating system will “trust” certificates issued by any of the certificate authorities whose public keys it includes in its own keystore. Certificates issued by any other CA’s will not be recognized and will be treated as “self-generated”.
Note, as in the example from the image above, that a certificate authority might have more than one public key included in a given browser or operating system with different expiration dates, different purposes, and different technical details.
And now for the real-world complexities
So far, the theoretical model is very elegant but the real world is never so simple. There are a few choices to be made that impact how well the system works.Key-Length
When one creates an encryption key it is necessary to decide how long the key will be. Longer keys are harder to guess, allow for more secure encryption, and will be considered safe longer. However, the length of the key also determines how lengthy the encryption process is. Some algorithms can only handle key sizes up to a given size. In some cases, extremely long keys would make encryption too slow without providing significant benefit. In extreme cases, longer keys would mean that some devices or older software cannot handle the key.Shorter keys will be faster to use but if you make a key too short it will weaken the protection of the encryption.
Certificate Authorities have guidelines for minimum and maximum length of Keys they will accept and they change over time. Keys that were considered “too long” a few years ago are now considered “too short to be secure”. At any point in time there is a range of acceptable key-lengths, and that range changes over time.
Encryption and Key-Generating Algorithms
Similar to key-length, new algorithms are being invented that might provide better security or need less resources to process, at the same time vulnerabilities in older algorithms sometimes make digital certificates insecure even before they have reached their planned expiration date.
Lost or stolen private keys
The security of this system depends on private keys being controlled by the person identified in a certificate. It is possible though that the computer that had the private key is destroyed, or worse it could be compromised and someone else could get access to the private key.
Bad Security Practices might be discovered
Some Certificate Authorities, through mistake or negligence, have been found to do things that compromise the integrity of certificates they issue. Imagine if we discovered that a CA had incorrectly given certificates to someone claiming to be a well-known bank but it is later discovered it was really a scammer trying to set up a fake look-alike site to steal the bank’s users’ credentials.
Certificate Revocation
For the reasons listed above, and a few others, it is sometimes necessary to revoke a digital certificate before it reaches its expiration date.Certificate Authorities keep track of all certificates they created that have been revoked and provide a revocation check mechanism. Part of the certificate validation process is to contact the CA that issued the certificate and ask what certificates have been revoked.
Rather than having every browser [10] contact a CA every time that they need to validate a certificate it is common to use local copies of revocation lists. When a browser needs to validate a digital certificate, it will ask the CA not only about that certificate but for a complete list of all the certificates that it has revoked. The browser will then save the list and use that for a while instead of contacting the CA for every certificate. For many programs, the default setting is to trust the list for up to one hour. Any certificate from that CA presented during that hour will be checked against the local copy. After one hour, the list is considered too old and is discarded. The next request will cause the browser to request a fresh copy of the list [11].
When a CA issues a digital certificate, it also gives the owner of the new certificate, instructions on how to ask for the certificate to be revoked if it becomes compromised.
In extreme cases, if a Certificate Authority itself is compromised, developers of Browsers might stop including that Certificate Authority’s public keys and therefore stop trusting all certificates issued by that CA.
Certificate Chains
Certificate Authorities don’t use the same private key to sign every certificate issued under their name. What they do is create intermediate certificates and even intermediate certificate authorities. This means that they used one of their “master” private keys to generate certificates that, amongst their permissions have “generate other certificates under my name”. In some cases, those other intermediate certificates had some restrictions like “This is only valid to generate digital certificates for a given geographic location”. For large companies, it might even be possible to get a “generic” digital certificate that say something like “can be used to generate TLS certificates for any website that ends in xyz.com”. They would give that intermediate certificate to an administrator of company xyz, and that administrator could then create certificates for www.xyz.com, support.xyz.com, mail.xyz.com, etc. without having to go through a separate validation process for each.This means that the validation is not simply from the certificate that you receive to one of the public keys that ships with your browser. It follows the chain of certificates, validating each in turn, until you reach a public key that ships in your browser. For this reason, the certificates in the browser are also called “root certificates”.
Note that if any certificate in the chain is revoked, expired, issued (signed) with an algorithm that is no longer trusted, or missing the “can generate sub-certificates” permission, the whole chain from that point on gets broken and none of the final (or leaf) certificates issued through that chain will be considered valid.
Time-Stamping
Updating a TLS certificate once a year or so usually doesn’t involve too much work as it is stored in a centralized location. Signed code however is copied and distributed to many locations, frequently outside of a single organization. Updating signed code requires re-distribution of the signed code. In some cases, signed code is meant to be authenticated and used unchanged for a long time. Since code-signing certificates are issued for only 1 to 3 years it is sometimes necessary to distribute an update to the code where the only difference between the current version and the updated one is a new signature.
To extend the useful lifetime of a digital signature, and therefore minimize the number of times that code has to be signed, the concept of Timestamping was introduced.
The idea behind timestamping is that, if something is signed before the certificate used for signing expires, and the certificate has not been revoked it is ok to continue trusting the signature even after the certificate expires. The problem then is how to validate that something was signed before the certificate expired.
Some Certificate Authorities created time-stamping services. They generate a digital certificate with a very long lifetime, sometimes up to ten years rather than the usual 1 to 3 years. They offer a mechanism for anyone to send the hash of a digital signature. The time-stamping service then appends the current time to the received hash and digitally signs both together with its own private key effectively creating a time-stamp that says: “this signature existed at this point in time.” [12] The signed code then adds this time-stamp to the signature as proof that the signature existed at that point in time.
The time-stamping service however is subject to the same rules of expiration and revocation so the time-stamp itself will eventually become invalid [13]. Time-stamping certificate expiration however should happen very infrequently so the need to redistribute code with only the signature updated could be drastically reduced (but not eliminated!) [14].

Footnotes
[1] This is simplified! If you need to learn more details there are plenty of technical sites available to you. I meant to give you a high-level understanding so we can talk about expiration dates and algorithm strengths... not to let you debate technical details with an expert in this field.[2] This one is one of the oldest encryption algorithms. It is believed that Julius Caesar used it over 2000 years ago. See https://en.wikipedia.org/wiki/Caesar_cipher . Modern algorithms are a lot more complicated.
[3] They are not really unrelated but you can’t calculate one if you only know the other one.
[4] The only thing that makes one key “private” and the other one “public” is which one I choose to share. There is nothing different between them that would make it so that I would have to choose one over the other for “private".
[5] In practice, it would take too long to encrypt anything but a small message with asymmetric encryption so it is more common to simply make up a random symmetric key, use that for encrypting the message with a faster algorithm, and only encrypt the made-up key using asymmetric cryptography.
[6] Unique meaning the same message will always result in the same value, not that another message couldn’t have the same value.
[7] Or rather would take a very fast computer longer than the age of the universe to try enough values to have a good enough chance of guessing.
[8] When systems use passwords for authentication it is common to store a hash of the password, rather than the actual password, in case the database storing them is compromised. Applications calculate the hash of user-entered passwords and compare hashes instead of comparing actual passwords.
[9] Although we could encrypt the complete message rather than just a checksum, since the message might be long, and asymmetric encryption is slow, it ends up being more efficient to encrypt only a checksum of the message.
[10] Browser, or OS, or Runtime. Whomever is validating the certificate.
[11] There are some improvements like OCSP Stapling that make this process less cumbersome but the overall idea is the same: Somehow check to see if the certificate is revoked before trusting it. See https://en.wikipedia.org/wiki/OCSP_stapling.
[12] Note that the time-stamping service only receives a hash, not the complete document, not even the complete signature that is being time-stamped. It time-stamps “whatever hash you pass” regardless of whether it’s really a hash for a signature or a random set of characters. It doesn’t know or care.
[13] It is possible to daisy-chain time-stamps, certifying that a time-stamp was valid with a newer time-stamp before the original time-stamping server expires. Not all program can validate daisy-chained time-stamps though and it will still be necessary to redistribute the code with the newer time-stamp. In most cases it is easier to simply re-sign from scratch. [back]
[14] To learn about time-stamping in more detail an interesting resource is https://www.nsoftware.com/kb/articles/legacy/sbb/11-timestamping.rst?page=all although it is meant to explain how a particular product uses Time-Stamping it does a good job at describing the underlying processes. [back]